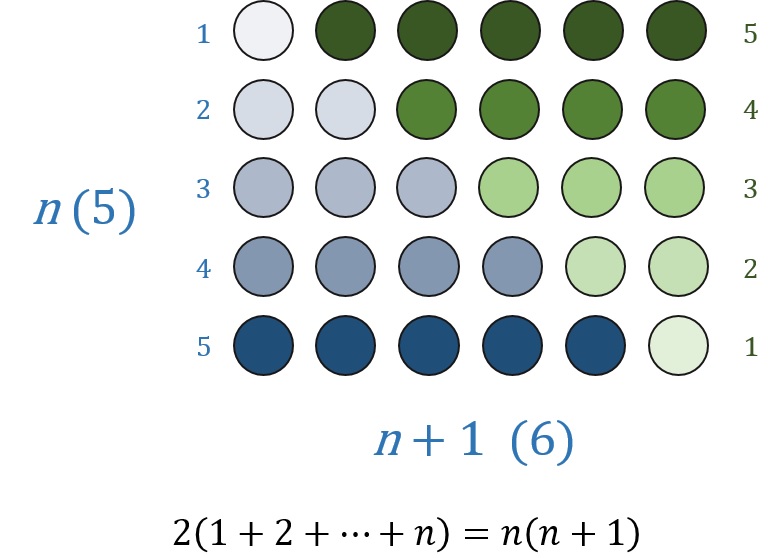En matemáticas se ha acuñado la expresión “demostraciones sin palabras” para designar a diagramas, esquemas o dibujos que, aunque no son realmente demostraciones, nos ayudan a comprender por qué un teorema es cierto o encierran la idea de la verdadera demostración matemática. Además, las “demostraciones sin palabras” son siempre sugerentes, atractivas y todo un ejercicio de estímulo para el pensamiento.
Como comenta el matemático Roger B. Nelsen, autor de los dos libros Proofs without words publicados por la Mathematical Association of America, se fueron haciendo populares a raíz de su publicación, a partir de 1975, en revistas como Mathematics Magazine y The College Mathematical Journal, primero como imágenes de relleno entre artículos y posteriormente como secciones fijas.
Como ejemplo de demostración sin palabras veamos la prueba visual, e incluso táctil, de la fórmula de la suma de los cuadrados de los n primeros números naturales, publicada por Man-Keung Siu en 1984 en Mathematics Magazine. Realizaremos el esquema de esta demostración sin palabras para n = 4. Para empezar, consideramos tres copias de una cierta estructura geométrica, realizada con cubos del material Live Cube, que refleja la suma de los cuadrados de los 4 primeros números 12 + 22 + 32 + 42 = 1 + 4 + 9 + 16 cubos.

Después, se juntan las tres estructuras para formar una estructura compacta.

Los cubos de dicha estructura forman un ortoedro, es decir, un prisma recto de base rectangular, cuya base tiene n = 4 cubos de ancho y n + 1 = 5 cubos de largo, y con una altura de n = 4 cubos, luego n (n + 1) n = 80 cubos en total. Además en la parte de arriba del ortoedro hay 1 + 2 + 3 + 4 cubos más (en general, 1 + 2 + … + n cubos), que aún no habíamos contado.
Teniendo en cuenta la conocida fórmula de la suma de los n primeros números enteros naturales, 1 + 2 + … + n = n (n + 1) / 2, se obtiene, contando la cantidad de cubos que hay en la estructura de las dos formas explicadas, que
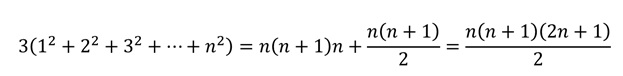
Si no conocíais la fórmula de la suma de los n primeros números enteros naturales, aquí os dejo una sugerente demostración sin palabras…