
Arthur Cayley. Fuente: https://commons.wikimedia.org/wiki/File:Arthur_Cayley.jpg
Por Raúl Ibáñez, profesor de Geometría y Topología de la UPV
Arthur Cayley (1821-1895) fue el matemático puro por excelencia de la Gran Bretaña del siglo XIX y uno de los matemáticos más prolíficos de todos los tiempos, con 976 artículos publicados y un libro. Investigó en todas las ramas de la matemática pura, pero sin lugar a dudas sus contribuciones más importantes fueron en álgebra, siendo uno de los artífices del nacimiento del álgebra moderna, y de la geometría. Su nombre está asociado al teorema de Cayley-Hamilton del álgebra matricial, a los determinantes, a los números de Cayley de la teoría de álgebras, al origen de la teoría de invariantes, al teorema de Cayley de teoría de grupos, a los espacios multidimensionales, a la noción de distancia en los espacios proyectivos y las geometrías no euclídeas, a la geometría algebraica con sus estudios sobre curvas y superficies cúbicas o a la fórmula de Cayley para árboles etiquetados.
En 1857, Arthur Cayley inventó un juego de cartas, relacionado con las permutaciones, al que llamó «La ratonera» (Un problema sobre permutaciones, Quart. Math. J.). En este juego se necesitan n cartas numeradas del 1 a n, por ejemplo 13, como en la baraja francesa. Se barajan bien las cartas, es decir, formando de este modo una permutación de las n cartas o, equivalentemente, del conjunto {1, 2, …, n}. Se coge el mazo de las n cartas barajadas, con los números hacia abajo, y se empiezan a coger las cartas, una a una, por la parte de arriba, a la vez que se va contando. Primera carta “1”, segunda carta “2”, tercera carta “3”, etcétera. Si el número de la carta que se coge coincide con el número que se está contando se retira dicha carta y se empieza a contar de nuevo desde “1” con la siguiente carta de arriba. En caso contrario, se coloca la carta en la parte de abajo del mazo y se continúa contando. Se gana en La ratonera si se terminan retirando todas las cartas, pero si se llega a contar hasta n + 1 (14 en el caso de 13 cartas) se habrá perdido.
Supongamos que se juega con 5 cartas, de forma que tras barajar quedan en el siguiente orden, de arriba abajo 3, 2, 5, 4, 1 (como en la imagen), se descarta primero la carta 2, después la carta 5, seguida de la carta 3 y ya no se puede descartar ninguna carta más. Mientras que con la posición inicial 4, 2, 3, 5, 1, se van descartando las cartas 2, 4, 5, 1 y finalmente la carta 3, con lo que se gana en el juego.

La cuestión que se plantea en relación a este juego es conocer para cuántas de las permutaciones posibles, es decir, formas de barajar las cartas, se puede ganar en la ratonera, y en general, para cuántas permutaciones quedarán solamente un número k de cartas. Por ejemplo, para n = 4, las permutaciones {1, 2, 4, 3} y {2, 1, 3, 4} son ganadoras, mientras que {1, 2, 3, 4} y {3, 2, 1, 4} no, en la primera solo se elimina la carta 1 y en la segunda las cartas 2 y 1. Además, Cayley muestra las permutaciones para las que las cartas se van retirando en el orden natural creciente, jugando desde con 1 hasta 8 cartas: {1}, {1, 2}, {1, 3, 2}, {1, 4, 2, 3}, {1, 3, 2, 5, 4}, {1, 4, 2, 5, 6, 3}, {1, 5, 2, 7, 4, 3, 6} y {1, 6, 2, 4, 5, 3, 7, 8}.
Y en la nota Sobre el juego de la ratonera (Quart. Math. J., 1878), Cayley analiza completamente el caso de 4 cartas. Para las 24 permutaciones de las 4 cartas, se descartan las siguientes cartas:
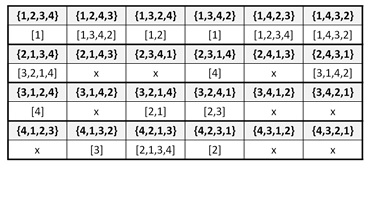
Luego, existen 6 juegos ganadores para la ratonera de 4 cartas, 3 para los que se descartan 2 cartas, 6 para los que se retira una sola carta y 9 para los que no se puede retirar ni una sola carta.




