“Más de mil tipos distintos de ramos de rosas” es el lema de una floristería. Está escrito en letras grandes y llamativas en la cristalera de la tienda, para captar la atención de todas las personas que pasan por el exterior de la misma. Los ramos de rosas son su producto estrella. Estos están formados por doce rosas, las cuales pueden ser de color rojo, blanco, rosa, amarillo, naranja o azul, y la cantidad de rosas de cada color en un ramo cualquiera varía entre ninguna, cuando ese color no forma parte del ramo, y doce, cuando el ramo es monocolor. Los dueños de la floristería afirman que se pueden componer más de mil tipos distintos de ramos de rosas, pero ¿cuántos tipos de ramos distintos son exactamente?
Esta cuestión puede plantearse matemáticamente. Si llamamos x, y, z, r, s, t a las variables que nos indican la cantidad de flores de cada color (respectivamente, rojo, blanco, rosa, amarillo, naranja y azul) que puede haber en un ramo de rosas, la cantidad de ramos distintos que se pueden componer es igual a la cantidad de soluciones de la ecuación
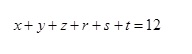
Una de las cuestiones interesantes de este problema matemático, calcular las soluciones de la anterior ecuación lineal, es que se puede resolver de una forma sencilla y hermosa, que consiste en sustituir las soluciones numéricas de la ecuación por diagramas de puntos y líneas, y contar cuántos diagramas existen.
Una solución de la ecuación anterior puede interpretarse como hacer seis grupos a partir de un conjunto de doce objetos. La cantidad de objetos de cada grupo representa el valor de cada variable, luego el número de rosas de cierto color en el ramo. En el diagrama se considera que los objetos son los puntos y se utilizan las líneas verticales para separar los seis grupos. Así, a la solución (1, 3, 2, 4, 1, 1) –que se corresponde con el ramo de una rosa roja, tres blancas, dos rosas, cuatro amarillas, una naranja y una azul– se le asocia el diagrama •|•••|••|••••|•|•. Es decir, las líneas verticales separan tantos puntos como el número correspondiente de la solución, dentro del total de doce puntos. De igual forma, la solución (5, 3, 2, 0, 2, 0) tiene asociado el diagrama •••••|•••|••||••|, (3, 1, 2, 3, 1, 2), el diagrama •••|•|••|•••|•|•• y (6, 3, 0, 0, 0, 3), ••••••|•••||||•••.
Por lo tanto, para generar cada diagrama debemos colocar un punto o una línea en los diecisiete (doce más cinco) «lugares» posibles, cinco huecos para las líneas y doce para los puntos. Como basta con determinar los lugares de las líneas, puesto que el resto serán para los puntos, la solución es la cantidad de formas en se pueden elegir cinco «lugares» dentro de los diecisiete posibles, cuestión clásica de la combinatoria, que nos dice que es el conocido número combinatorio 17 sobre 5, C(17,5),
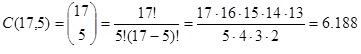
Por lo tanto, el número de tipos distintos de ramos de rosas posibles, con doce rosas que pueden ser de color rojo, blanco, rosa, amarillo, naranja o azul, es mayor de mil, exactamente 6.188 tipos distintos.
Este razonamiento, con diagramas de puntos y líneas, nos permite demostrar el resultado general (teorema) sobre ramos distintos de n rosas con hasta k colores distintos, o soluciones de la correspondiente ecuación lineal:

¿Qué solución de la ecuación lineal prefieres tú?




