Si existe una sucesión de números enteros que se puede decir que “todo el mundo conoce”, esa es la sucesión de Fibonacci, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … que fue introducida por el matemático italiano Leonardo de Pisa (1170-1241), conocido como Fibonacci (hijo de Bonaccio), en su libro Liber Abaci – El libro del ábaco (1202), como solución a un problema de ingenio, el famoso problema de los conejos.
A partir de entonces, se convirtió en un tema de interés dentro de las matemáticas, y posteriormente, también de la sociedad en su conjunto, formando parte incluso de todo tipo de obras artísticas. Como es conocido, cada término de la sucesión fn se obtiene como suma de los dos términos anteriores, es decir, fn = fn-1 + fn-2, para n = 0, 1, 2,… Sin embargo, no todo el mundo sabe que esta sucesión ya era conocida varios siglos antes de Fibonacci por los estudiosos indios de la métrica en sánscrito.
En la poesía en sánscrito, lengua antigua y culta de la India, existían dos tipos de poemas, aquellos con un número fijo de sílabas por verso (llamados varna–vrttas), como en los sonetos, cuyos versos tienen 11 sílabas, y los que tenían un número fijo de “moras” (llamados matra–vrttas), como los haikus en la poesía japonesa. En sánscrito, como en algunas otras lenguas, existían dos tipos de sílabas, unas cortas (llamadas laghu), con una mora, o tiempo silábico, y otras largas (llamadas guru), con dos moras.
Los estudiosos de la métrica en sánscrito analizaban las posibles estructuras que se producían en ambos tipos de poemas. Por ejemplo, si llamamos C a una sílaba corta y L a una larga, un verso de tipo varna–vrttas de tres silabas tiene 8 estructuras posibles, en función de sus moras: CCC, LCC, CLC, CCL, CLL, LCL, LLC y LLL. Luego, el número de sílabas se mantiene, pero no el de moras, que va desde 3 hasta 6, según la estructura. Pero, veamos cuántas estructuras posibles existen para los versos matra–vrttas, para versos con 1, 2, 3, 4 o 5 moras.
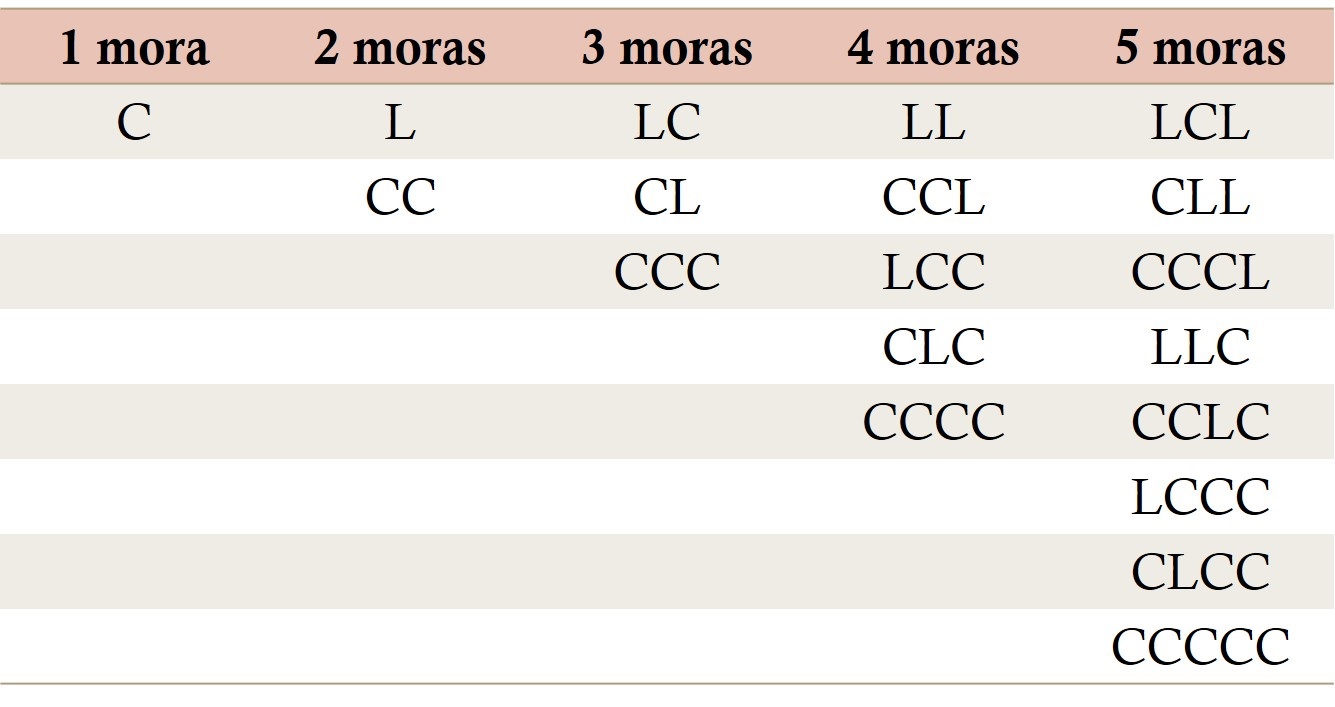
El número de variaciones posibles, para versos con 1, 2, 3, 4 o 5 moras, es 1, 2, 3, 5 y 8, que son números de Fibonacci. Pero fijémonos, por ejemplo, en las estructuras de los versos con 4 moras, los podemos dividir en dos tipos, los que terminan en una sílaba larga (L), que son las dos estructuras con 2 moras (L y CC) a las que se ha añadido dos moras mediante una sílaba larga (LL y CCL), y los que terminan en una sílaba corta (C), que son las tres estructuras con 3 moras (LC, CL y CCC) a las que se ha añadido una mora mediante una sílaba corta (LCC, CLC y CCCC). En consecuencia, hay 2 + 3 = 5 posibles estructuras con 4 moras.
Si ahora quisiéramos ver cuántas estructuras diferentes existen para los versos de la métrica matra–vrttas con 6 moras, obtendríamos que son 13, los generados a partir de los de 4 moras al añadirle una sílaba larga (L), que son 5, y los generados a partir de los de 5 moras al añadirles una sílaba corta (C), que son 8, luego en total 5 + 8 = 13. En concreto, LLL, CCLL, LCCL, CLCL y CCCCL, junto con LCLC, CLLC, CCCLC, LLCC, CCLCC, LCCCC, CLCCC y CCCCCC.
Por tanto, lo que estamos diciendo es que el número de estructuras posibles con m moras es igual a la suma del número de estructuras con m – 1 y m – 2 moras, que es el motivo por el que salen los números de Fibonacci. En resumen, ¡la cantidad de estructuras posibles para versos matra–vrttas con m moras es igual al número de Fibonacci Fm!
¿Desde cuándo se conocía este hecho? Aunque hay quien piensa que la primera autoridad en el estudio de la métrica en sánscrito Acarya Pingala, que vivió entre el 700 a.c. y el 100 d.c., ya era conocedor de esta realidad, lo cierto es que el primer texto en el que se explica la regla de formación del número de estructuras de matra–vrttas fue Acarya Virahanka, quien vivió entre los siglos sexto y octavo. En una de sus obras puede leerse algo así: “Juntando las variaciones de las dos métricas anteriores, se obtiene la cantidad. Este es un método para conocer el número (de variaciones) de la siguiente matra–vrtta”. Otros estudiosos incluso mencionaron explícitamente la sucesión de números “1, 1, 2, 3, 5, 8, 13, 21, …”.




