Por Fina Arévalo, Gerente de Ciencias de SM
Comienzo esta entrada con un agradecimiento y reconocimiento a dos personas. A Luis Berenguer, a quien conocí hace casi 10 años en las XIII Jaem. Él me inspiró y enseñó que “otra manera de aprender es posible”. Desde entonces y hasta ahora, he estado buscando y aprendiendo a hacer matemáticas, grandes matemáticas, con los más pequeños y con materiales sencillos. Cada vez que nos volvemos a ver, aprendo algo de nuevo, gracias a su generosidad y sencillez. Esa misma generosidad y sencillez la vivo desde hace años cada día de Javier Bernabeu, que me enseña cada día cosas nuevas. Su cabeza, en constante ebullición, no para de buscar nuevas maneras para comprender y hacer matemáticas. Muchísimas gracias a los dos.
Esa nueva visión de Luis Berenguer me hizo buscar, leer, desaprender, aprender,… Piaget, Bruner, Vigotsky,… hablan de la necesidad de que el niño vaya “desde lo concreto hasta lo abstracto” y de que “todo pensamiento matemático surge de acciones, y los conceptos matemáticos tienen su origen en los actos que los niños lleva a cabo con los objetos”; es decir que lo que importa del uso de cualquier material son las acciones sobre el material, no el material en sí mismo. Es el niño quien con sus acciones sobre los materiales va descubriendo y estableciendo relaciones y las formula en su lenguaje. Por tanto, debemos huir de la tentación de transmitir o contar ese concepto, intentando que haya menos enseñanza y más aprendizaje, así como de la utilización de los materiales para una mera comprobación de resultados, y que sí sean el vehículo de un pensamiento más profundo y significativo.
El material que os proponemos trabajar hoy, son las plaquetas de Herbinière Lebert, que desarrolló Suzanne Herbinière Lebert allá en los años 50 para trabajar los números y el cálculo en edades tempranas.
Hace no mucho, conseguí hacerme con el material del profesor de las plaquetas de Herbinière Lebert y algunos manuales, dónde se explicaba o explotaba el uso de este material.
Al igual que las regletas Cuisenaire, permiten construir los números por composición y descomposición y conduce de manera natural a presentar el concepto del número estableciendo relaciones de suma y de resta.
Partiremos de algo más concreto como bolitas de papel, canicas, …y comenzaremos a establecer la unidad, oponiéndola a «varios» o a «muchos». Les enseñaremos una bolsa con muchas canicas 
dentro. Le preguntaremos: ¿Cuántas canicas hay? Y ellos dirán: muchas. Sacaremos alguna canica de la bolsa y les volvemos a preguntar, ¿cuántas canicas hay ahora? Ellos contestarán que menos, pero todavía hay muchas. Repetiremos el proceso hasta que solo quede 1 en la bolsa y volveremos a preguntar. Contestarán: una bolsa canicas
Ahora le añadiremos otra canica y les preguntaremos, algunos dirán que es dos, otros, varias, pero dirán que este varias es más pequeño que muchos. Si surgen dudas en diferenciar dos y muchos, podemos preguntarles ¿qué prefieres tener, dos o muchos? Y enseguida se genera un debate y se llega rápidamente a diferenciar dichos conceptos.
Un paso intermedio, antes de trabajar con las plaquetas, es que ellos representen con gomets lo que acaban de descubrir con las canicas. Los puntos les llevarán fácilmente a trabajar con las plaquetas.
Podemos hacerlo de manera inversa y pedirles que representen con los gomets uno, dos y muchos:
Una vez familiarizados con estos conceptos y la representación, ya podemos repartirles las plaquetas y empezar a establecer la unidad. Para descubrir el número 2 o cualquier número lo hacemos por iteración de la unidad, añadiendo una unidad.
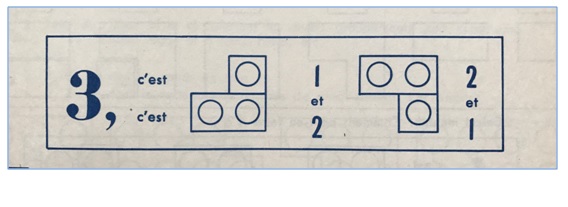
¡Vamos a por el 3 con el material del profesor!
Podríamos hacerlo como un 1 y 1 y 1, pero si le pedimos a los niños que lo hagan con el menor número de piezas posible, podemos partir del 2 (ya conocido) y le añadimos otra unidad. Pedir al alumno que encuentre una plaqueta que coincida con la figura.
A partir de aquí algún alumno podría haber representado de otras formas el número 3 y se ha introducido de manera natural o implícita la propiedad conmutativa, sin utilizar “palabros” innecesarios.
Así, podemos construir cada plaqueta añadiendo un elemento o unidad a los ya conocidos, así el niño descubre intuitivamente el principio de la base de la numeración, la sucesión de los números se crea al añadir una unidad. Esto puede parecer un trabajo repetitivo o monótono o tener la sensación de que se está perdiendo el tiempo, pero como dijo Rousseau: «el mejor modo de ganar tiempo es saber perderlo».
Para comprobar que el niño ha interiorizado la forma de construcción de los números podemos realizar las siguientes actividades:
- Ordenar las plaquetas en orden creciente y decreciente, asociando una tarjeta con la cifra correspondiente.
- Mostrar una plaqueta al azar y que el niño muestre la tarjeta con la cifra correspondiente. También puede indicar oralmente el número que corresponde.
- Decir un número y que el niño muestre la plaqueta correspondiente.
- Mostrar una placa y preguntar: ¿cuál es el número anterior? ¿y el siguiente? Una vez se domine esas actividades, ahora sin mostrar el material, preguntar ¿qué números van después del 4? ¿y antes?, …
Es muy importante tener en cuenta que la acción debe anteceder a la verbalización y esta a la escritura. Por ello, en este momento que ya hemos comprendido los números podemos comenzar con su grafía. Otra actividad importante son las distintas descomposiciones que puede tener cada plaqueta de manera inmediata, como por ejemplo:
De manera manipulativa, hemos introducido el concepto de suma a partir de la acción de unir y juntar. No es necesario definirlo, pero sí escribimos simbólicamente lo que se ha hecho manipulativamente. Para asegurarnos de que lo han entendido podemos preguntarles: ¿qué haremos si ponemos + 3?
Una vez dominado este proceso, podemos realizar actividades de manera recíproca:
- Mostrad la plaqueta resultante de hacer 2 + 3.
- Representar 5 sin usar la plaqueta del 5.
Hasta aquí la primera parte del trabajo que podemos realizar con este material. Hay mucha gente que le da importancia en este material a la fácil identificación de los números pares e impares, aunque a mí me parece anecdótico frente al potencial que tiene. Os dejo aquí la representación de los números. A ver si podéis explicarme con palabras de niños qué os sugiere esta imagen.
