El número π es una de las constantes matemáticas más importantes que existen, pero además es un número fascinante que goza de una gran popularidad entre el público, tanto el matemático, como el no matemático. No en vano tiene dos celebraciones internacionales en su honor, el “Día de pi” (14 de marzo, 3-14 en inglés) y el “Día de aproximación de pi” (22 de julio, en referencia a la aproximación dada por Arquímedes, 22/7 = 3,1428…).
La relación entre la longitud de una circunferencia y su diámetro, que es como se define el número π, tiene unos 4.000 años de antigüedad. Sin embargo, hasta el año 1.761 no se consiguió demostrar, por el matemático francés Johann H. Lambert (1728-1777), que este es un número irracional. Lo cual significa que π no se puede expresar como el cociente entre dos números enteros, o equivalentemente, si consideramos su expresión decimal, esta tiene infinitos decimales y no es periódica, es decir, no existe un número finito de decimales –conocido como período– que, a partir de un decimal dado, se repita de forma infinita, contrariamente a lo que ocurre con números como 146/825, que es racional y cuya expresión decimal es 0,17696969…, siendo su período 69.
De hecho, la búsqueda de los decimales del número π es una investigación activa hoy en día. Se trata de conocer todos los decimales posibles de π (recordemos que todos es imposible, son infinitos y no hay un patrón finito que se repita). El record de decimales en la actualidad es de … 22.459.157.718.361 dígitos … obtenido por Peter Trueb en 2016.
Por otra parte, podemos preguntarnos, entre los decimales del número π, que son infinitos y sin un patrón finito que se repita, cuáles de las diez cifras básicas 0, 1, 2, …, 9 aparece con más frecuencia, y cuales, con menos, dentro de la expresión decimal del número π, o si por el contrario todas las cifras aparecen en la misma proporción. Si miramos a los 100 primeros decimales del número π,
3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679…
observaremos que las diez cifras básicas, del 0 al 9, aparecen en la siguiente proporción: 8, 8, 12, 11, 10, 8, 9, 8, 12, 14. Si las diez cifras básicas aparecieran en la misma proporción, tendrían que aparecer diez veces cada cifra básica en los 100 primeros números, aunque la verdad es que 100 decimales no son muchos, y necesitaríamos ver más decimales. Por tanto, ¿qué ocurre para 1.000, 10.000, 100.000, o más, decimales?
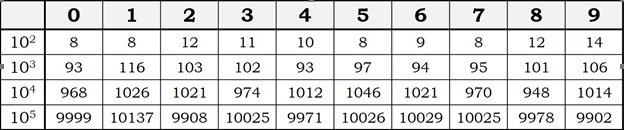
Como podemos observar en la tabla anterior, según va aumentando el número de decimales, la proporción de cada una de las diez cifras básicas dentro de los decimales del número π se van acercando al 10% de los decimales.
En el artículo Digit Statistics of the First 22.4 Trillion Decimal Digits of Pi, su autor, Peter Trueb, nos confirma este hecho entre los 22.459.157.718.361 decimales que se han calculado de la constante geométrica. Más aún, si se toman las 100 secuencias de dos dígitos formadas por las diez cifras básicas, del 00 al 99, cada una aparece en una proporción que se va acercando cada vez más a 1/100, es decir, un 1%. Y lo mismo ocurre para las 1.000 secuencias de tres dígitos, de 000 a 999, cada una de las cuales aparece en una proporción que se va aproximando a 1/1.000. Todas las secuencias posibles son igualmente probables.
Todo esto lo que nos está diciendo es que aparentemente el número π podría ser lo que se conoce como un “número normal” (para la base 10), y que fue introducido por el matemático francés Émile Borel (1871-1956), en 1909. Sin embargo, a día de hoy demostrar la normalidad de π sigue siendo un problema abierto. La supuesta normalidad del número π es lo que nos permite afirmar que dada una secuencia finita de dígitos, como nuestro NIF o número de móvil, llegará un momento entre los decimales de pi en que aparecerá. En internet existen páginas para buscar “tus” números en pi, por ejemplo, subidiom.
La artista donostiarra Esther Ferrer nos acerca a la propiedad de normalidad de π, mediante un contundente argumento visual en el cual asigna un color a cada cifra básica, en su excelente obra Pi (2009-2010). Inspirado por su trabajo os traigo aquí los 399 (más el 3 inicial) decimales del número π, asignando un color distinto a cada una de las cifras básicas.