Por Javier Bernabeu, editor del Equipo de Matemáticas de SM.
Las tablas se pueden razonar y se deben razonar. No hay un único camino para multiplicar. ¿Por qué nos empeñamos en enseñar a los niños nuestro camino?
Consejo 1. Adiós a la memorieta
Forzar a un niño a memorizar las tablas de multiplicar ordenadas, desordenadas, de atrás hacia adelante y de adelante a atrás es como si, de repente, a nosotros nos hacen memorizar esto:
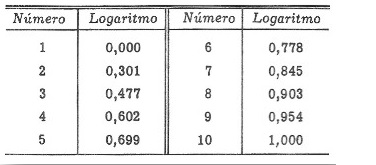
O esto otro:
Con buena capacidad memorística podemos ser capaces de memorizar los logaritmos de los 10 primeros números y podemos ser capaces de memorizar la lista de los reyes Godos.
Pero… ¿Y si falla la memoria?
Las “tablas” se pueden razonar y se deben razonar. Entrecomillo “tablas” porque con los consejos que daré a continuación no hay tabla que aprender, simplemente aprenderemos a resolver productos (resolveremos de igual manera 7 × 8 o 32 × 8).
He mentido un poquito en el párrafo anterior. Sí hay algunas “tablas” que aprender. Les pediremos que aprendan esas que menos les cuestan: la del 1, la del 2 y la del 5.
Consejo 2. ¿Qué debe saber el niño antes de enfrentarse a las multiplicaciones?
El alumno debe dominar la suma. Con esto no quiero decir que vayamos a recurrir a esas gigantescas sumas para resolver 8 × 7 (8 + 8 + 8 + 8 … o 7 + 7 + 7 + …) ¡Nada de eso, por favor!
Debemos dominar la suma para poder encontrar atajos rápidos que permitan llegar al resultado deseado.
Debemos trabajar previamente la suma en línea y de izquierda a derecha. Esto es un trabajo que debería iniciarse en primero de primaria, aunque nunca es tarde.
Ejemplos:
34 + 20 es 50 y 4 que es 54
25 + 32 es 50 y 7 que es 57
46 + 14 es 50 y 10 que es 60
47 + 34 es 70 y 11 que es 81
Lógicamente, para poder resolver las sumas descritas anteriormente el niño debe dominar la suma de números de una cifra. En la mayoría de los casos, el problema en las aulas es que se abandona rápido el trabajo con números de una cifra. Pero, como he dicho antes, nunca es tarde.
Consejo 3. Ya sabe sumar… ¿Y ahora qué?
Antes de empezar a resolver multiplicaciones como locos, vamos a ver si saben jugar a la palabra prohibida:
– Profesor: Juan, ¿cómo dices 3 sin decir 3?
-Juan: ¡2 y 1!
-Profesor: Rosa, ¿cómo dices 7 sin decir 7?
-Rosa: ¡4 y 3!
-Profesor: Rosa, ¿y eres capaz de decir 7 diciendo 5?
-Rosa: ¡5 y 2!
Las dinámicas de descomposición son fundamentales, pues es el recurso que utilizaremos para resolver cualquier multiplicación.
Consejo 4. Transformando multiplicaciones desconocidas en otras conocidas
Retomamos aquellas tablas que hemos quedado que aprenderían (la del 1, la del 2 y la del 5).
Empezamos resolviendo… ¡7 x 4!
No me sé la tabla del 7, no me sé la tabla del 4 y no queremos sumar 7 veces el 4 ni 4 veces el 7.
Elegimos uno de los dos factores y lo descomponemos utilizando uno, dos o cinco.
Supongamos que descompongo el 4 en 2 y 2. En ese caso hemos hecho esta transformación:
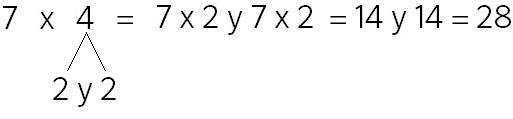
La tabla del 2 era una de las que me sabía así que puedo resolver 7 x 2 y 7 x 2 que es 14 y 14 (que sé hacerlo porque sumé muchos números de dos cifras de izquierda a derecha) que es 28.
Otro niño puede elegir descomponer el 7 en 5 y 2 y resolver de este modo:
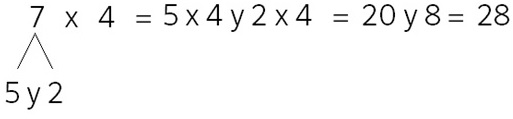
Abordar de manera exhaustiva el sentido numérico trabajando con números conectados es un estupendo recurso para aprender las tablas de multiplicar.
En el proyecto “Piensa Infinito” (metodología Singapur), de la editorial SM, se le da especial importancia a los números conectados, propiciando que los alumnos lleguen por diferentes caminos a los mismos resultados. Pero la representación que se hace en el mismo de los números conectados no es exactamente como ves arriba, sino que metemos la descomposición en círculos y no mezclamos letras con símbolo. Adaptado a Singapur sería algo así:
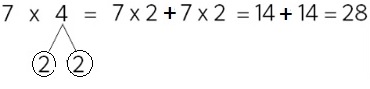
No hay un único camino ¿Por qué nos empeñamos en enseñar a los niños nuestro camino?
¡Esta manera de multiplicar lleva mucho tiempo. Es un proceso ineficaz!… Aclararemos un par de cosas antes de realizar tamaña afirmación:
- El proceso que se está llevando a cabo servirá para todos los cálculos futuros (incluyendo la temida división entre varias cifras).
- El alumno no tiene por qué escribir el desarrollo (aunque no hay problema en hacerlo).
- El alumno no deja ningún producto en blanco. Llega al resultado de manera muy razonada.
- El alumno es libre de elegir su camino.
He hecho un poco de trampa porque he puesto un ejemplo de la tabla del 7 y, claro, 7 es 5 y 2 que son las que se saben… (Es difícil identificar la ironía en un escrito. Este comentario de la tabla del 7 es irónico, ya que la tabla del 7 es la más complicada para los niños).
Vamos a por otro ejemplo:
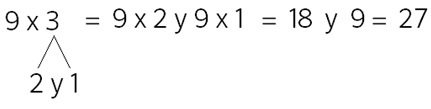
Otros pueden llegar descomponiendo el 9 en 5 y 2 y 2 y dirían: 15 y 6 y 6 que también es 27.
Consejo 5. Ya tienes confianza… ¡Estúdiate otra!
Ya sabes las tablas del 1, del 2 y del 5. Con esto puedes construir lo que quieras pero, a veces, es un rollo multiplicar por 8, porque habría que descomponer en 5 y 2 y 1 o en 2 y 2 y 2 y 2 …
Ya hemos cogido confianza y podemos enfrentar al reto de aprender la tabla del 3. Insisto en que no es necesario, pero es cómodo trabajar con el 3 para algunas descomposiciones. Y, dado que sé que es la última que tendré que estudiar, es un reto muy asumible.
Si sé la tabla del 3, puedo llegar por varios caminos a ese producto que, por algún misterioso motivo, muchos niños olvidan siempre… ¡8 x 7!
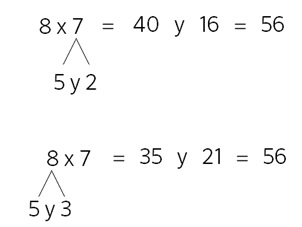
Es difícil de creer que multiplicar por descomposición es más rápido que hacerlo de memorieta, pero, creedme, si la suma de números de dos cifras está bien trabajada es mucho más rápido y da igual qué multipliquemos por 7 o por 57.
Consejo 6. Da igual lo que necesites resolver… ¡Mira!
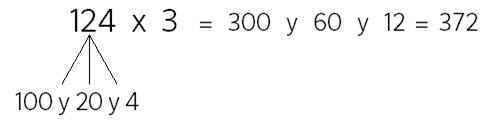
¿Un poquito más difícil? Ahí va…

¡Os he engañado un poco de nuevo! Para resolver la de arriba hay que saberse la tabla del 10… ¡Y esa no era de las que había que estudiar!
¿En serio conocéis a algún niño que no sepa la tabla del 10?
Y hablando de tabla del 10… Ahí va el séptimo consejo.
Consejo 7. El misterioso hueco en las multiplicaciones por varias cifras
Cuando un niño se enfrenta por primera vez a una multiplicación por dos cifras ocurre que no sabe colocar bien los sumandos, y suele olvidarse de saltarse “el huequito” pero… ¿y si no dejamos el huequito?
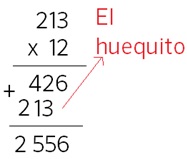
Los niños están tan acostumbrados a eso de “unidades con unidades” y “decenas con decenas” que no saben por qué en el caso anterior eso no pasa…
¿Recordáis que en el consejo anterior multiplicamos 213 x 12 en línea descomponiendo el 12 en 10 y 2? Pues ese exactamente es el motivo del huequito:
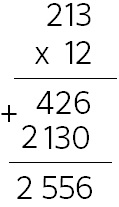
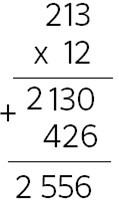
Multiplicar por 12 es multiplicar por 10 y por 2 y cualquier número natural multiplicado por 10 acaba en cero… ¿Qué motivo hay para no poner el cero?
Por cierto, si ponemos el cero, da igual multiplicar primero por 10 y luego por 2 o primero por 2 y luego por 10, ya que se cumple la propiedad conmutativa.
Todo lo descrito anteriormente está ampliamente contrastado con cientos de alumnos que he tenido en los últimos 15 años, y muchos profesores con los que he compartido este tipo de estrategias en los últimos cinco años.
Ayudemos a nuestros niños a pensar, a razonar y, solo si eso no es posible (cosa que dudo), tiremos de memorieta… Nada de memorieta. En caso de ser necesario, vayamos a una memoria comprensiva.




